石鑫华视觉
描述镜头成像质量的内在指标是镜头的光学传递函数与畸变,但对拥护而言,需要了解的仅仅是镜头的空间分辨率,以每毫米能够分辨的黑白条纹线对为计量单位,计算公式为:镜头分辨率N=视野总线数/2/画幅格式(L/W)。如500W像素镜头,2/3’传感器,则有2448/2/8.8=139线对/毫米。石鑫华视觉网提供。
光学仪器形成分立图像能力的定量度量,又称分辨率。由于镜头(光瞳)对光束的限制而产生的衍射效应,使物点发射的光波在像面上不可能成为一个像点,而是以像点为中心扩展为一定的强度分布,其中心斑就是夫琅和费衍射的零级斑,也叫做爱里斑。这就是说,即使不考虑所有几何像差,成像光学仪器也无法实现点物成点像的理想情况。因此,物面上相距很近的两个分离的物点,在像面上就可能成为两个互相重叠的衍射斑,这两个衍射斑甚至可能过度重叠,变得模糊一团,以致观察者无法辨认物方两个物点的存在。总之,物方图像是大量物点的集合,而变换到像面上的强度分布却是大量衍射斑的集合,它不可能准确地反映物面上的所有细节。为了给光学仪器规定一个分辨细节能力的统一标准,通常采用瑞利判据。瑞利判据规定,当一个像斑中心刚好落在另一个像斑边缘(即一级暗环)时,确认两个像斑刚刚可以分辨(见图b)。计算表明,满足瑞利判据时的两个像斑强度的不相干叠加的结果,其光强起伏量约为20%,正常人眼是能分辨这种光强差别的。当然对于客观的光接收器如乳胶底片、光电管之类,或其他传感器来说,也许并不苛求20%的起伏量作为它的可分辨的界限,但瑞利判据仍不失之作为一个相对标准,用以估算和比较光学仪器的分辨本领。
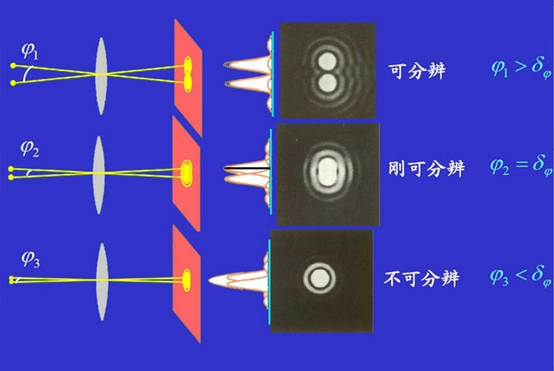
分辨本领
人眼眼瞳的直径De可在2~8mm范围内调节。根据瑞利判据,并由爱里斑的半角宽度公式,可以求得人眼的最小分辨角公式为
δθe=1.22λ/ De
以 De=2mm,光波长λ=0.55μm估算,人眼的最小分辨角数值为3.355*10-4弧度(弧度=角度/180°*PI)
δθe≈1’=0.075mm/25cm=3mm/10m
即正常人能分辨明视距离25cm处相隔 0.075mm的两条刻线,或者说,能分辨10m远处相隔3mm的两条刻线。生理光学的这一数据对于助视光学仪器和电视机的设计,以及对于图像识别这类问题,都是必须考虑的基本数据。
望远镜 它观察的对象是远物,其本身线度并不小,故通常以最小分辨角δθm直接标志它的分辨本领。望远镜的最小分辨角公式为
δθm≈1.22λ/D(弧度)
式中λ为媒质中的光波长,D为光瞳(物镜)的直径。以D=2000mm,λ=0.55μm估算,δθm≈0.06″。为减少δθm以提高分辨本领,必须加大物镜口径。由于光波在长程传输过程中受大气扰动的影响,天文望远镜的实际分辨本领比上述理论分辨本领要低。因此,每个国家都尽可能地将大型的天文望远镜设在高山顶上。中国云南天文台设在海拔 2300m的山顶上。美国于1981年在夏威夷建成的一台红外望远镜,直径为3357mm,设在海拔4200m的山顶上,它可观测几十亿光年远的天体,用来研究一般光学望远镜不易观测的天体的分子结构和正在形成过程中的星体外壳。
显微镜
它的观察对象是细小的近物,故通常以最小分辨距离 δym直接标志它的分辨本领。根据瑞利判据以及爱里斑的半角宽度公式,并考虑到显微镜工作在齐明点,可以导出显微镜的最小分辨距离公式为
δym≈0.61λo/(n*sinuo)
式中 n为物方折射率,uo为物光束的孔径角,λo为真空波长,乘积nsinuo称为数值孔径,用N.A.表示。作为一种数量级的估算,数值孔径最大不超过N.A.≈n≈1.5(油浸镜头),故δym有个限度
δym≥0.4λo,
在可见光波段, δym≥0.2μm。为了充分发挥显微镜的分辨能力,应将δym放大到足以使眼睛可分辨的距离δye≈δθe×25cm≈0.075mm,由此估算光学显微镜的横向线放大率v≈δye/δym≈400倍。当然过高的放大率也没有必要,此时仪器仍然无法分辨δym以下的细节。这个与分辨本领相匹配的放大率称为显微镜的正常放大率或有效放大率。设计时一般选用放大率稍大于正常放大率,光学显微镜的放大率不超过1000倍。进一步提高显微镜分辨本领的惟一途径是缩短波长。近代电子显微镜利用电子束的波动性经“磁透镜”成像,电子束的波长很短(取决于加速电压),可达┱量级,不过电子束的孔径角也小(不到10°),其结果可使电子显微镜的分辨本领比光学显微镜的高几个数量级,相应的放大率可达数万倍至百万倍,能显示蛋白质分子结构。
摄影系统
摄影系统(如照相机、电视摄像机一类)一般工作于远物短焦距情形,它与助视光学仪器(望远镜、显微镜)不同之点在于,物经摄影镜头成为一个缩小的实像被感光介质直接记录。因此,在分析整个系统的分辨本领问题时,既要考虑到镜头(光瞳)的衍射效应,又要考虑到记录介质本身的空间分辨率N──感光乳剂单位长度内能分辨的线纹数目。镜头衍射效应限制的物方最小分辨角公式仍然是δθe=1.22λ/ D,在像面上的摄影系统的最小分辨线度相应地为δy’m≈1.22λf/D,式中f为镜头焦距,比值D/f称为镜头的相对孔径。相对孔径越大,则镜头的分辨本领越高。以相对孔径1∶3.5估算,δy’m ≈2.35 μm。为了充分利用镜头的分辨本领,记录介质的分辨率应满足N≥1/δy╭≈425mm-1,即要求选用每毫米能分开425条线纹以上的感光乳剂。
以上给出的光学成像仪器的分辨本领的公式是仅考虑衍射效应以后的理论公式,而实际上成像仪器还有各种各样的几何像差,对摄影系统尤其如此,所以仪器的实际分辨本领比理论值要低一些,有些甚至降低一个量级。将破坏点物成点像的各种因素综合起来,统一地对成像质量作出评价的工作开始于50年代兴起的光学传递函数的概念。